Nowadays, the relational model is the essential data model for commercial data processing applications, which achieved its primary position because of its simplicity, which makes the job of the programmer easy, in contrast to earlier data models such as the network model or the hierarchical model. In this chapter, you will study the essential and primary uses of the relational model. A substantial theory exists for relational databases.
The Relational Database Management System (RDBMS) has become the leading data-processing software in use nowadays with approximated new license sales of between US$6 billion and US$10 billion per year. This software signifies the second generation of DBMSs and is based on the relational data model proposed by Mr. E. F. Codd in the year 1970.
What is Relational Model?
The relational model is the theoretical basis of relational databases, which is a technique or way of structuring data using relations, which are grid-like mathematical structures consisting of columns and rows. Codd proposed the relational model for IBM, but the idea became extremely vital and prominent that his work would become the basis of relational databases. You might be very familiar with the physical demonstration of a relation in a database - which is known as a table.
In the relational model, all data is logically structured within relations, i.e., tables, as mentioned above. Each relation has a name and is formed from named attributes or columns of data. Each tuple or row holds one value per attribute. The greatest strength of the relational model is the simple logical structure that it forms. Behind this simple structure is a sophisticated theoretical foundation that is lacking in the first generation of DBMSs.
Objectives of the Relational Model
The relational model's objectives were specified as follows:
- To allow a high degree of data independence, application programs must not be affected by alterations to the internal data representation, mostly by changes to file organizations or access paths.
- To provide considerable grounds for dealing with data semantics, reliability, and redundancy problems. In particular, Codd's theory for the relational model introduced the concept of normalized relations, were relations that have no repeating groups, and the process is called normalization.
- To allow the expansion of set-oriented data manipulation languages.
Real-life Structure of a Relational Database
In general, a row in a table signifies a relationship among a group of values. Since a table is a collection of such relationships, there is a close connection amongst the concept of the table and the mathematical concept of relation, from which the relational data model gets its name. In mathematical terminology, a tuple is simply a sequence or list of values. A relationship between n values is indicated mathematically by an n-tuple of values, i.e., a tuple with n values, corresponds to a row in a table.
Database Schema
When you talk about the database, you must distinguish between the database schema, which is the logical blueprint of the database, and the database instance, which is a snapshot of the data in the database at a given instant in time. The concept of a relation corresponds to the programming language notion of a variable. In contrast, the concept of a relation schema corresponds to the programming languages' notion of the type definition. In other words, a database schema is a skeletal structure that represents the logical view of the complete database. It describes how the data is organized and how the relations among them are associated and formulates all the constraints that are to be applied to the data.
In general, a relation schema consists of a directory of attributes and their corresponding domain.
Some Common Relational Model Terms
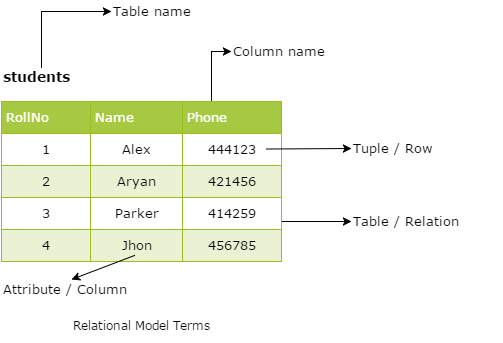
- Relation: A relation is a table with columns and rows.
- Attribute: An attribute is a named column of a relation.
- Domain: A domain is the set of allowable values for one or more attributes.
- Tuple: A tuple is a row of a relation.