Linked lists are a fundamental data structure that is the foundation for various complex data structures and algorithms. Unlike arrays, linked lists are dynamic and efficient in managing collections of elements. This tutorial will dive into the concept, implementation, and operations of linked lists, focusing on their significance in data structures.
What is a Linked List?
A linked list is a sequence of elements, known as nodes, where each node is connected to the subsequent node via a pointer. The list is characterized by its head (the first node) and its tail (the last node, which points to null), facilitating dynamic data management. Linked lists are preferred for their efficient insertion and deletion operations, especially when compared to array-based structures.
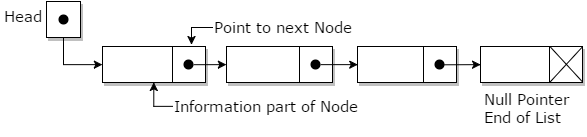
Characteristics of Linked Lists
- Dynamic sizing: Automatically resizes, overcoming the fixed-size limitation of arrays.
- Efficient operations: Adding or removing nodes at the beginning or end can be done in constant time, O(1).
- Sequential access: Nodes are accessed sequentially, making search operations linear time, O(n).
Implementing a Linked List
Implementing a linked list involves defining a node structure and a linked list class to manage nodes. Let's break down the implementation:
The Node Structure
Begin by defining a node, the fundamental building block containing the data, and a pointer to the subsequent node.
struct Node {
int data;
Node* next;
Node(int data) : data(data), next(nullptr) {}
};
The Linked List Class
The linked list class organizes node management, insertion, searching, and deletion methods.
class LinkedList {
Node* head;
Node* tail;
public:
LinkedList() : head(nullptr), tail(nullptr) {}
void insertAtEnd(int data);
bool search(int data);
bool deleteNode(int data);
};
Insertion at the End
This insertion operation appends a new node and adjusts the tail's next pointer.
Algorithm for Insertion at the End:
Algorithm InsertAtEnd(data)
1. Initialize newNode with data.
2. If head is NULL, then
a. Set head and tail to newNode.
3. Else,
a. Set tail's next to newNode.
b. Update tail to newNode.
End Algorithm
Example:
void LinkedList::insertAtEnd(int data) {
Node* newNode = new Node(data);
if (!head) {
head = tail = newNode;
} else {
tail->next = newNode;
tail = newNode;
}
}
Searching for a Value
To search for a value, iterate through the list until the value is found or the list ends.
Algorithm for Searching for a Value:
Algorithm Search(data)
1. Initialize current to head.
2. While current is not NULL,
a. If current's data equals data, return true.
b. Move current to the next node.
3. Return false.
End Algorithm
Example:
bool LinkedList::search(int data) {
Node* current = head;
while (current) {
if (current->data == data) return true;
current = current->next;
}
return false;
}
Deletion of a Node
Deleting a node requires locating it and adjusting pointers to remove it from the list.
Algorithm for Deletion of a Node:
Algorithm DeleteNode(data)
1. Initialize current to head and prev to NULL.
2. While current is not NULL and current's data is not data,
a. Set prev to current.
b. Move current to the next node.
3. If current is NULL, return false (node not found).
4. If current is head, update head to current's next.
5. Else, set prev's next to current's next.
6. If current is tail, update tail to prev.
7. Delete current.
8. Return true.
End Algorithm
Example:
bool LinkedList::deleteNode(int data) {
Node *current = head, *prev = nullptr;
while (current && current->data != data) {
prev = current;
current = current->next;
}
if (!current) return false; // Node not found
if (current == head) head = current->next; // Node is head
else prev->next = current->next; // Node is in the middle or end
if (current == tail) tail = prev; // Node is tail
delete current;
return true;
}
Conclusion
Linked lists are a cornerstone of data structure with their dynamic sizing and efficient element operations. This tutorial taught you the basics of linked lists, including their structure, implementation, and core operations. As you become more comfortable with linked lists, you'll find them invaluable for solving a wide range of problems in computer science.