Polynomials and Sparse Matrix are two critical applications of arrays and linked lists. A polynomial comprises different terms, each with a coefficient and an exponent. This tutorial includes the representation of polynomials using linked lists and arrays.
What is a Polynomial?
A polynomial 'p(x)' is an expression in variable ' taking the form '(axn + bxn-1 + …. + jx+ k)', where 'a, b, c ….', k are real numbers, and ' is a non-negative integer known as the degree of the polynomial. Each term in a polynomial comprises a coefficient and an exponent.
Example: In the polynomial '10x2 + 26x', 10 and 26 are coefficients, and 2 and 1 are their respective exponents.
Key Points in Polynomial Representation
- Coefficients and exponents are stored with their signs.
- Polynomials may have terms with equal exponents.
- Terms are typically arranged in order of descending or ascending exponent value.
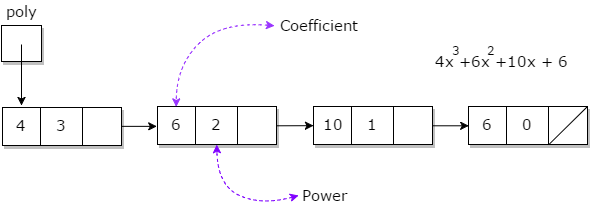
Representation of Polynomials
Depending on the specific requirements, polynomials can be efficiently represented using either arrays or linked lists.
Representation of Polynomials Using Arrays
Arrays provide a straightforward approach for representing dense polynomials, where a polynomial of degree 'n' is stored in an array of length 'n+1'. Each array index corresponds to an exponent, with its value representing the coefficient. Here is the C++ code for polynomial addition using Arrays:
Example:
#include <iostream>
#include <vector>
using namespace std;
class Polynomial {
private:
vector<int> coeffs; // Vector to store coefficients, index is the exponent
public:
// Constructor initializes the polynomial with a given degree
Polynomial(int degree) : coeffs(degree + 1, 0) {}
// Function to insert or update a term in the polynomial
void insertTerm(int coefficient, int exponent) {
// Ensure the vector is large enough to hold this exponent
if (exponent >= coeffs.size()) {
coeffs.resize(exponent + 1, 0);
}
coeffs[exponent] = coefficient; // Set coefficient for the given exponent
}
// Function to add another polynomial to this one
void addPolynomial(const Polynomial& other) {
// Resize the current polynomial if it's smaller than the other
if (other.coeffs.size() > coeffs.size()) {
coeffs.resize(other.coeffs.size(), 0);
}
// Add coefficients of the other polynomial to this one
for (size_t i = 0; i < other.coeffs.size(); ++i) {
coeffs[i] += other.coeffs[i];
}
}
// Function to display the polynomial
void display() const {
bool firstTerm = true;
for (int i = coeffs.size() - 1; i >= 0; --i) {
if (coeffs[i] != 0) {
if (!firstTerm) {
cout << " + ";
}
cout << coeffs[i] << "x^" << i;
firstTerm = false;
}
}
cout << "\n";
}
};
int main() {
Polynomial poly1(2); // Initialize polynomial of degree 2
poly1.insertTerm(3, 2); // Insert 3x^2
poly1.insertTerm(4, 1); // Insert 4x^1
Polynomial poly2(3); // Initialize polynomial of degree 3
poly2.insertTerm(5, 3); // Insert 5x^3
poly2.insertTerm(1, 2); // Insert 1x^2
cout << "Polynomial 1: ";
poly1.display();
cout << "Polynomial 2: ";
poly2.display();
// Add poly2 to poly1
poly1.addPolynomial(poly2);
cout << "Result after addition: ";
poly1.display();
return 0;
}
Output:
Polynomial 1: 3x^2 +4x^1
Polynomial 2: 5x^3 +1x^2
Result after addition: 5x^3 +4x^2 +4x^1Representation of Polynomial Using Linked Lists
Linked lists are ideal for representing polynomials where non-zero coefficients are rare or when dynamic manipulation (such as adding new terms) occurs frequently. Here is the C++ code for polynomial addition using linked lists:
Example:
#include <iostream>
using namespace std;
// Define a structure for a polynomial term
struct PolynomialTerm {
int coefficient;
int exponent;
PolynomialTerm* next;
PolynomialTerm(int coeff, int exp) : coefficient(coeff), exponent(exp), next(nullptr) {}
};
// Define a class to represent and manipulate a polynomial
class Polynomial {
private:
PolynomialTerm* head;
public:
Polynomial() : head(nullptr) {}
// Function to insert a new term to the polynomial
void insertTerm(int coefficient, int exponent) {
// Create a new term
PolynomialTerm* newTerm = new PolynomialTerm(coefficient, exponent);
// Insert in sorted order of exponents
if (!head || head->exponent < exponent) {
newTerm->next = head;
head = newTerm;
} else {
PolynomialTerm* current = head;
PolynomialTerm* prev = nullptr;
while (current && current->exponent > exponent) {
prev = current;
current = current->next;
}
// Combine terms with the same exponent
if (current && current->exponent == exponent) {
current->coefficient += coefficient;
delete newTerm;
} else {
newTerm->next = current;
if (prev) {
prev->next = newTerm;
}
}
}
}
// Function to add another polynomial to this polynomial
void addPolynomial(const Polynomial& other) {
PolynomialTerm* term = other.head;
while (term) {
insertTerm(term->coefficient, term->exponent);
term = term->next;
}
}
// Function to display the polynomial
void display() const {
PolynomialTerm* term = head;
while (term != nullptr) {
cout << (term != head && term->coefficient > 0 ? "+" : "") << term->coefficient << "x^" << term->exponent << " ";
term = term->next;
}
cout << "\n";
}
// Destructor to free dynamically allocated memory
~Polynomial() {
while (head) {
PolynomialTerm* temp = head;
head = head->next;
delete temp;
}
}
};
int main() {
Polynomial poly1, poly2;
// Insert terms to the first polynomial
poly1.insertTerm(3, 2); // 3x^2
poly1.insertTerm(4, 1); // +4x^1
// Insert terms to the second polynomial
poly2.insertTerm(5, 1); // 5x^1
poly2.insertTerm(1, 0); // +1
cout << "Polynomial 1: ";
poly1.display();
cout << "Polynomial 2: ";
poly2.display();
// Add poly2 to poly1
poly1.addPolynomial(poly2);
cout << "Result after addition: ";
poly1.display();
return 0;
}
Output:
Polynomial 1: 3x^2 +4x^1
Polynomial 2: 5x^1 +1x^0
Result after addition: 3x^2 +9x^1 +1x^0This code snippet demonstrates how to represent polynomials using linked lists in C++, offering a dynamic and efficient way to handle polynomials of varying degrees and sparse coefficients.
Conclusion
Both arrays and linked lists provide versatile options for representing polynomials in computer programs. Arrays are straightforward and efficient for polynomials with dense coefficients and known degrees. In contrast, linked lists offer flexibility and efficiency for sparse polynomials or when degrees vary widely, making them suitable for dynamic polynomial manipulations. Depending on the application's specific requirements, developers can choose the most appropriate data structure for polynomial representation.